How Zerocash works
Zerocash is a protocol that provides a decentralized crypto-currency in which, as in Bitcoin, users collaborate to maintain the currency by broadcasting and verifying payment transactions. Zerocash, however, differs from Bitcoin in how these payment transactions are assembled and then verified.
Concretely, in Bitcoin, a payment transaction consists of an origin address, destination address, and payment amount. These transactions are bundled into blocks and stored on a decentralized ledger called block chain. Because the block chain is public, the history of all transactions can be viewed by anyone, via the Bitcoin software or by visiting any block-chain monitoring service. While addresses are not explicitly tied to users' real identities, several recent works have shown that the block chain can be mined to learn information about users' spending habits.
Zerocash extends Bitcoin's protocol by adding new types of transactions that provide a separate privacy-preserving currency, in which transactions reveal neither the payment's origin, destination, or amount. Zerocash creates a separate anonymous currency, existing alongside a (non-anonymous) base currency, which we refer to as Basecoin. Each user can convert (non-anonymous) basecoins into (anonymous) Zerocash coins, which we call zerocoins. Users can then send zerocoins to other users, and split or merge zerocoins they own in any way that preserves the total value. Users can also convert zerocoins back into basecoins, though in principle this is not necessary: all payments can be directly made in terms of zerocoins.
Zerocash transactions
Zerocash's functionality is realized using just two new types of transactions: mint transactions and pour transactions. Like Bitcoin transactions, Zerocash transactions are broadcast and appended to a decentralized ledger.
Mint transactions. A mint transaction allows a user to convert a specified number of non-anonymous bitcoins (from some Bitcoin address) into the same number of zerocoins belonging to a specified Zerocash address. The mint transaction itself consists of a cryptographic commitment to a new coin, which specifies the coin's value, owner address, and (unique) serial number. The commitment is based on the SHA-256 hash function, and hides both the coin's value and owner address.
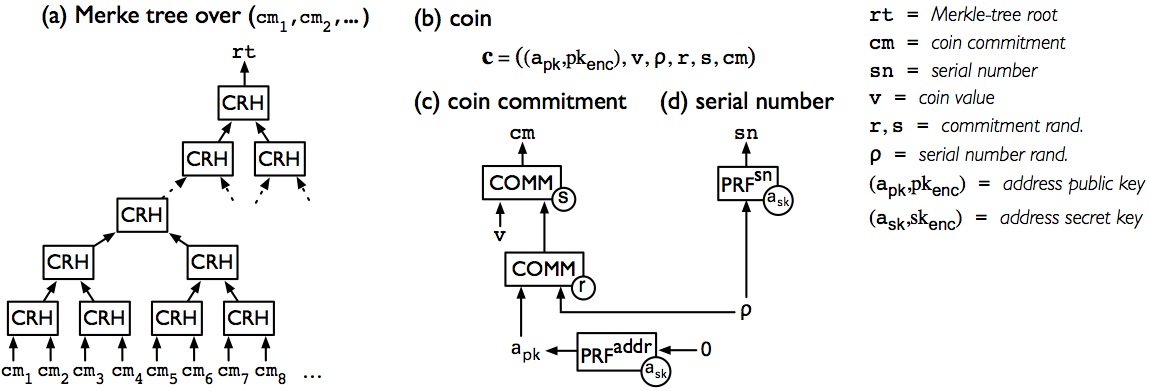
Individual Zerocash nodes maintain a Merkle tree over all of the coin commitments seen thus far. Any user can then demonstrate ownership of a coin commitment, via its decommitted values as well as a short witness of membership in the tree. Unfortunately, merely publishing this information as an "ownership proof" is not private; instead, to achieve privacy, we rely on a second type of transaction, which allows a user to prove, in zero knowledge, that he knows such information.
Pour transactions. A pour transaction allows a user to make a private payment, by consuming some number of coins (owned by this user) in order to produce new coins. Roughly, a pour transaction, for (up to) two input coins and (up to) two output coins, involves proving, in zero knowledge, that:
- the user owns the two input coins;
- each one of the input coins appears in some previous mint transaction or as the output coin of some previous pour transaction; and
- the total value of the input coins equals the total value of the output coins.
The pour transaction consumes the input coins by revealing their serial numbers, but does not reveal any other information such as the values of the input or output coins, or the addresses of their owners. Optionally, the pour transaction can also output some (non-anoymous) bitcoins. This last feature can be used to transfer zerocoins back into (non-anonymous) bitcoins or to pay transaction fees.
Verifying Zerocash transactions
For a mint transaction, the commitment contained therein is constructed so that that anyone can verify that the committed coin has the claimed value.
For a pour transaction, anyone can verify that the zero-knowledge proof contained therein is valid (and that a few other simple invariants hold). For efficiency, however, Zerocash does not use "any" zero-knowledge proof, but leverages zero-knowledge Succinct Non-interactive ARguments of Knowledge (zk-SNARK) systems, which are zero-knowledge proofs that are particularly short and easy to verify. Specifically, Zerocash uses zk-SNARKs constructed by SCIPR Lab, which are described in BCTV14; such proofs are less than 300 bytes long and can be verified in only a few milliseconds.
More details
See our technical paper!